Common formulations in linear algebra, regression and optimization, and dynamic systems

Linear system of equations

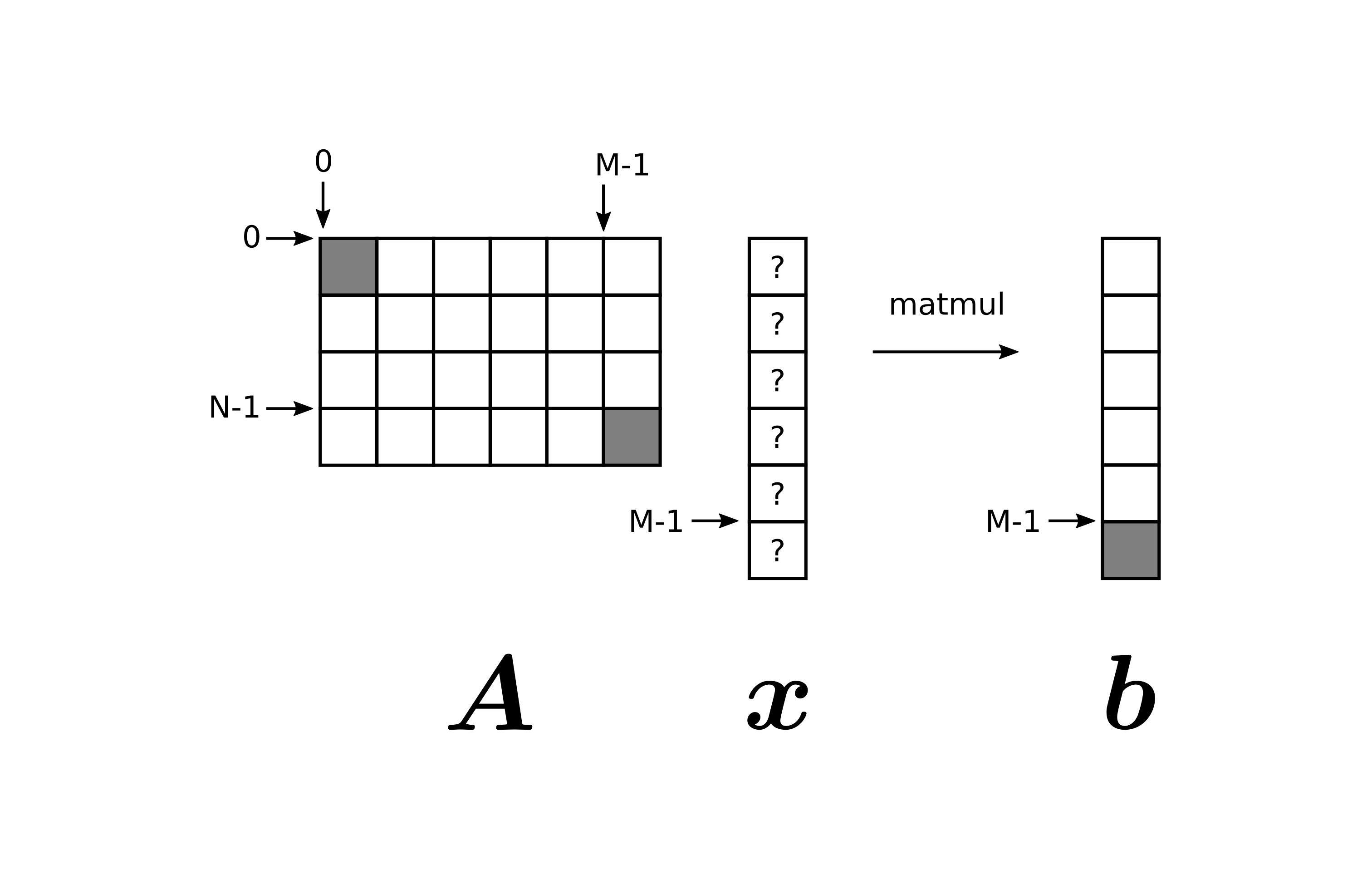
\[ \boldsymbol{A} \boldsymbol{x} = \boldsymbol{b} \]

A linear system of equations can be underdetermined or overdetermined.

Eigenvalue equations

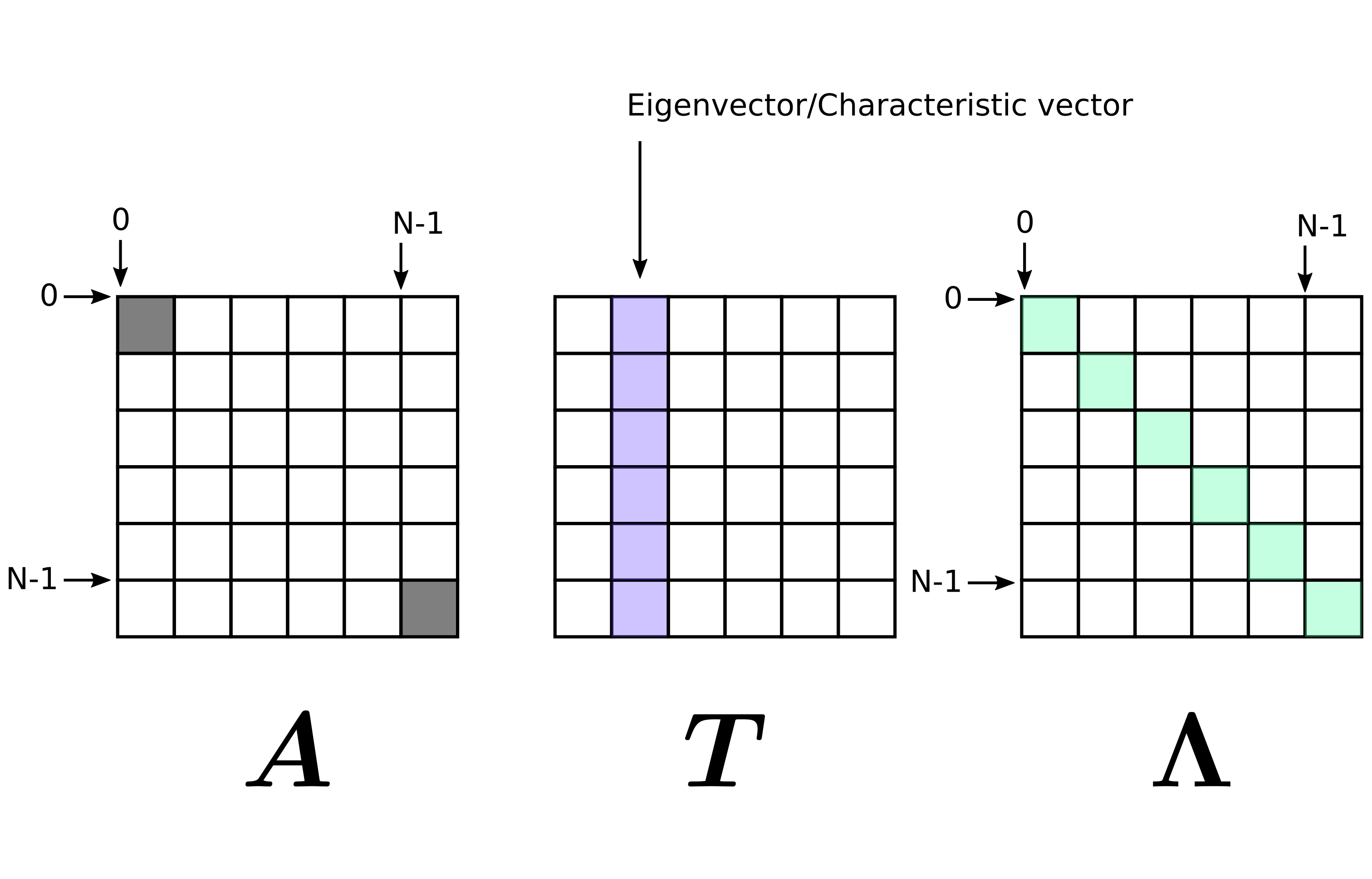
\[ \boldsymbol{A} \boldsymbol{T} = \boldsymbol{T} \boldsymbol{\Lambda} \]

Singular value decomposition (SVD)

\[ \boldsymbol{X} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^T \]

Overdetermined and underdetermined optimization for linear systems

\[ \underset{x}{\text{argmin}}( \Vert \boldsymbol{A} \boldsymbol{x} - \boldsymbol{b} \Vert_2 + \lambda g(\boldsymbol{x})) \] or \[ \underset{x}{\text{argmin}} \; g(\boldsymbol{x}) \; \text{subject to} \; \Vert \boldsymbol{A} \boldsymbol{x} - \boldsymbol{b} \Vert_2 \le \epsilon \]

\(\lambda\) is the regression penalty for overdetermined systems. The choice of penalty is also known as regularization.

Galerkin expansion

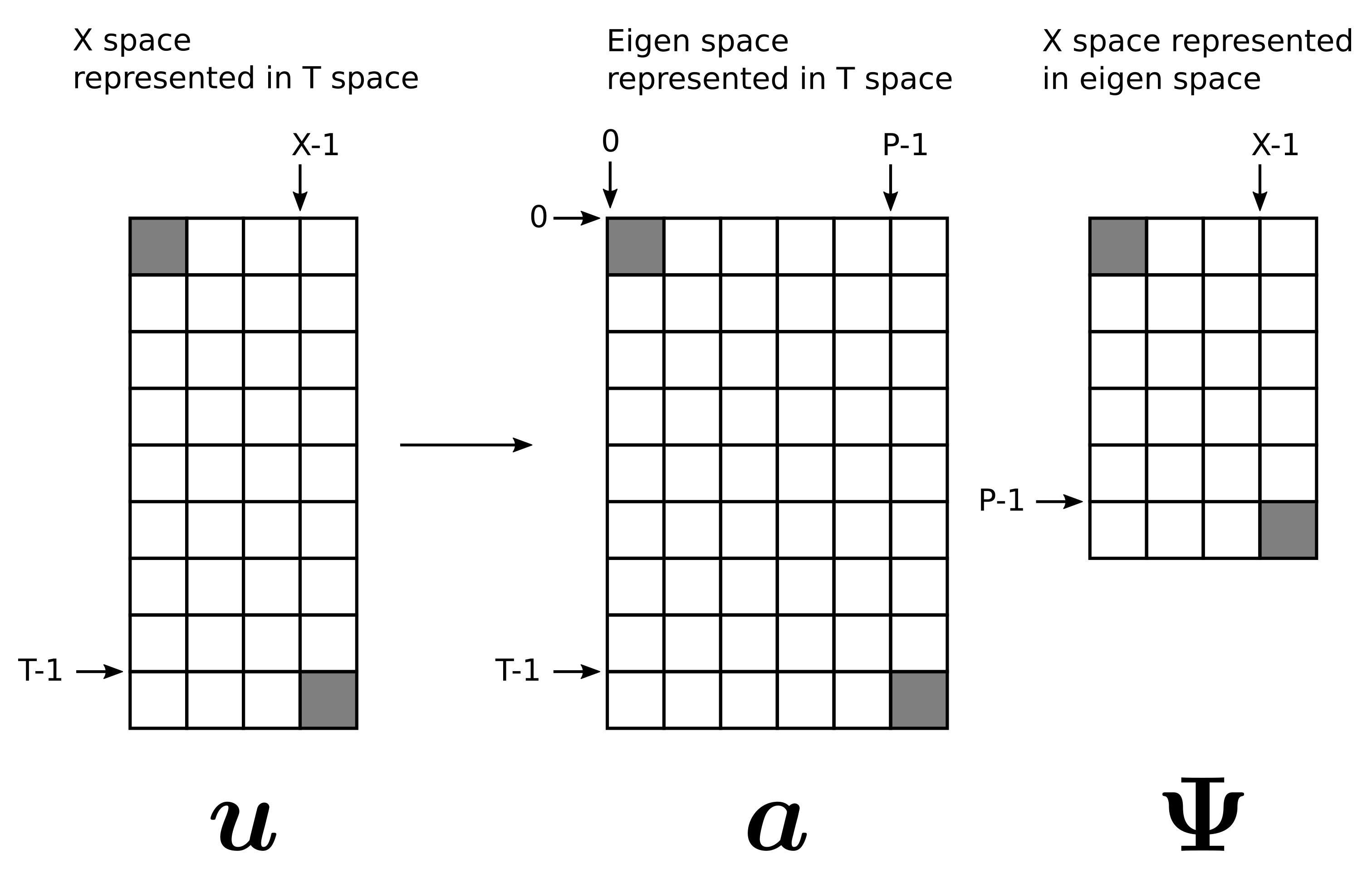
\[ u(x, t) = \sum_{k = 1}^{r} a_k(t)\psi_k(x) \]

\(a_k(t)\) are temporal coefficients that capture the time dynamics, and \(\psi_k(x)\) are spatial modes.